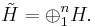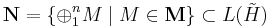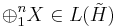Von Neumann bicommutant theorem
In mathematics, specifically functional analysis, the von Neumann bicommutant theorem relates the closure of a set of bounded operators on a Hilbert space in certain topologies to the bicommutant of that set. In essence, it is a connection between the algebraic and topological sides of operator theory.
The formal statement of the theorem is as follows. Let M be an algebra of bounded operators on a Hilbert space H, containing the identity operator and closed under taking adjoints. Then the closures of M in the weak operator topology and the strong operator topology are equal, and are in turn equal to the bicommutant M′′ of M. This algebra is the von Neumann algebra generated by M.
There are several other topologies on the space of bounded operators, and one can ask what are the *-algebras closed in these topologies. If M is closed in the norm topology then it is a C*-algebra, but not necessarily a von Neumann algebra. One such example is the C*-algebra of compact operators (on an infinite dimensional Hilbert space). For most other common topologies the closed *-algebras containing 1 are still von Neumann algebras; this applies in particular to the weak operator, strong operator, *-strong operator, ultraweak, ultrastrong, and *-ultrastrong topologies.
It is related to the Jacobson density theorem.
Proof
Let H be a Hilbert space and L(H) the bounded operators on H. Consider a self-adjoint subalgebra M of L(H). Suppose also, M contains the identity operator on H.
As stated above, the theorem claims the following are equivalent:
- i) M = M′′.
- ii) M is closed in the weak operator topology.
- iii) M is closed in the strong operator topology.
The adjoint map T → T* is continuous in the weak operator topology. So the commutant S’ of any subset S of L(H) is weakly closed. This gives i) ⇒ ii). Since the weak operator topology is weaker than the strong operator topology, it is also immediate that ii) ⇒ iii). What remains to be shown is iii) ⇒ i). It is true in general that S ⊂ S′′ for any set S, and that any commutant S′ is strongly closed. So the problem reduces to showing M′′ lies in the strong closure of M.
For h in H, consider the smallest closed subspace Mh that contains {Mh| M ∈ M}, and the corresponding orthogonal projection P.
Since M is an algebra, one has PTP = TP for all T in M. Self-adjointness of M further implies that P lies in M′. Therefore for any operator X in M′′, one has XP = PX. Since M is unital, h ∈ Mh, hence Xh∈ Mh and for all ε > 0, there exists T in M with ||Xh - Th|| < ε.
Given a finite collection of vectors h1,...hn, consider the direct sum
The algebra N defined by
is self-adjoint, closed in the strong operator topology, and contains the identity operator. Given a X in M′′, the operator
lies in N′′, and the argument above shows that, all ε > 0, there exists T in M with ||Xh1 - Th1||,...,||Xhn - Thn|| < ε. By definition of the strong operator topology, the theorem holds.
Non-unital case
The algebra M is said to be non-degenerate if for all h in H, Mh = {0} implies h = 0. If M is non-degenerate and a sub C*-algebra of L(H), it can be shown using an approximate identity in M that the identity operator I lies in the strong closure of M. Therefore the bicommutant theorem still holds.
References
- W.B. Arveson, An Invitation to C*-algebras, Springer, New York, 1976.